For my school assignment about animation trough code I started out by reading Foundation Actionscript 3.0 Animation: Making Things Move! by Keith Peters. Although this book focuses on AS3, the animation principles can be applied to all kind of programming/scripting language.

I tried to follow along with the examples from the book by converting (some of) the code to c++/openFrameworks. Not all examples where that exciting so I may have skip a couple. In part 3 of the book (Advanced Motion) things got a bit more interesting. And based on some techniques from that chapter I created a small program to see if I understood those principles.

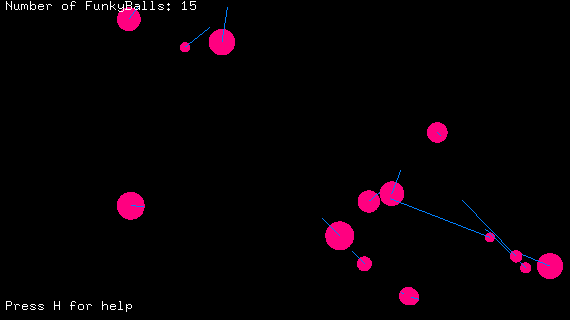
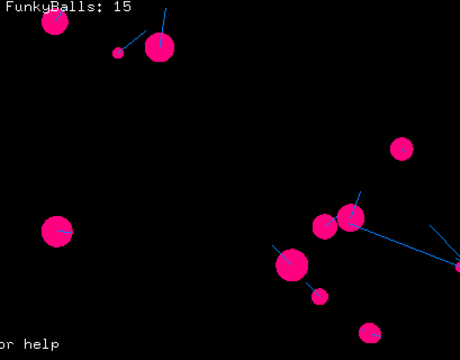
On the screen there live some 'funky'Balls, which will bounce around and bump into each other. When a ball is added to the screen it will get a random position, size and velocity vector (speed and direction). The velocity vector is represented by the blue line in this image (although its displayed amplified to make it more clear). The balls do also have a mass, which is the same as the surface area of the circle. This is used for calculating new positions of the balls in case of a collision based on the Law of Conservation of Momentum. Basically this means that when two balls collide there combined velocity before the collision is the same the the combined velocity (because there mass won't change).

Unfortunately this theory doesn't seem be correctly implemented by me, because when let the program run for a little while, especially when increasing the number of balls (by pressing +), some strange stuff will happen. Balls will get some insane velocity and bounce like maniacs. The log window shows the combined velocity, and if I'm right this should always be the same (if no balls are added or removed). But as you can see this isn't the case.

Keeping the balls from going really fast isn't that hard, you could easily add some sort of friction. But the main problem here is this Conservation of Momentum not working properly, or at least that's what I think.

Keith Peters notices some potential problems in his book, some of which you will see here as well. For example, balls that are getting stuck together. Also because of the way the collision detection works, balls will mostly only collide when they are already (partial) on top of each other. This may be the cause of the total velocity problem I described before.

Despite of the program being far from perfect I had to leave it (at least for now) like this. I'll need to protect myself from 'freaking' on one small issue, while there is still a lot of stuff to explore.

For those who like, here is the source code and compiled program (win32).